Modelos de inventario

Inventario:

Bienes que adquieren las empresas industriales o comerciales, para su posterior transformación o simple comercialización, respectivamente, lo cual constituye el objeto principal de las actividades primarias y normales de las entidades, es decir la obtención de ganancias derivadas de la venta de inventarios, que satisfagan las necesidades de los consumidores. 

¿Por qué existen los inventarios?

Para entenderlo propongamos un ejemplo:

Tengo una empresa que demanda diariamente 100 unidades de cierto insumo.

Supongamos que mi empresa tiene un proveedor de ese insumo en los Estados Unidos de América, con el cual mantiene buenas relaciones. Es un proveedor cuyos productos son de primera calidad, manteniendo un margen muy pequeño de productos defectuosos. El tiempo de entrega, sumado a los trámites de legalización del insumo que proveen es de 20 días. En tal caso la empresa debe mantener un inventario mínimo de 2000 unidades.

Pero el proveedor abre una sucursal en una ciudad dentro del país, a unos 1000 km de distancia. Ahora el margen de espera que promete la empresa es de tan solo 5 días. En tal caso el inventario mínimo debe ser de 5000 unidades, por lo cual la reducción es clara, ayudando a la empresa a disminuir costos de mantener ese inventario guardado.

La empresa proveedora tiene problemas en la instalación inicial de sus máquinas, por lo que algunas unidades están siendo fabricadas con defectos; mientras solucionan el problema tienen un porcentaje de unidades defectuosas de 10%, permitiendo que sus clientes conozcan el problema y devuelvan las unidades defectuosas con el camión que lleve el próximo pedido. Como en el pedido, el 10% de unidades puede ser defectuoso, no pueden pedir solo 5000 unidades, sino que su pedido debe ser ahora de 5555 unidades.

Después de cierto tiempo, la empresa compra un lote justo al lado de la planta de producción de mi empresa y por el buen pedido que hago construimos una banda transportadora que lleva los insumos directamente a la línea de producción. El inventario que ahora necesitamos será de 0 unidades!!!

Entonces….¿por qué existen los inventarios?

•        Razón 1. El inventario existe debido al tiempo de respuesta por parte del proveedor. Si el tiempo de respuesta de este es menor, el inventario necesario será menor, esto debido a que la empresa necesitará menos productos almacenados disponibles para operar normalmente.
•         Razón 2. Productos en inventario de calidad deficiente. La empresa necesita prever el suministro de insumos o materias primas inútiles, por parte del proveedor, por lo cual deberá conservar un inventario
  
  Gestión de inventario
  
  
  
  Para empezar en la gestión de inventarios, para entender los modelos, es necesario introducir el concepto de demanda. ¿Qué es demanda?
  
  
  
  
  Demanda se define como el consumo de un producto en un determinado tiempo.
  
  
  Según la teoría de inventarios, se conocen entonces dos modelos que involucran a la demanda.
  
  
  • Modelos determinísticos: en los cuales se conoce la demanda.
  • Modelos estocásticos: no se puede determinar con exactitud la demanda, por lo cual se trata como una variable aleatoria.
  
  
  Los inventarios, según la demanda se clasifica en:
  
  
  • Dependiente: en el cual la cantidad y precios ya están establecidos. Se estudia mediante MRP I – MRP II y ERP.
  • Independiente: sale directamente de la necesidad del mercado. Si esta es constante, todos los períodos será la misma. Si es variable, la demanda es aleatoria.
  
  
  Procederemos a estudiar, los inventarios con demanda independiente constante, la cual presenta distintos modelos.
  
  
  
  
   Modelo EOQ
  

  Economic

  Order

  Quantity

  El modelo EOQ, o Cantidad Económica de Pedido, busca encontrar el monto de pedido que reduzca al mínimo el costo total del inventario de la empresa.

  Se basa en tres supuestos fundamentales, el primero es que la empresa conoce cuál es la utilización anual de los artículos que se encuentran en el inventario, segundo que la frecuencia con la cual la empresa utiliza el inventario no varía con el tiempo y por último que los pedidos que se colocan para reemplazar las existencias de inventario se reciben en el momento exacto en que los inventarios se agotan.

   

  Modelo EOQ sin faltante planeado (básico)

  En base a los supuestos del modelo EOQ, se puede graficar el comportamiento de las cantidades en función del tiempo.

  

  
  

  Según el modelo EOQ, se conocen los valores del costo de la adquisición de productos (CuQ), el costo de pedirlo (Cp) y el costo de inventario (Cmi).

  Teniendo en cuenta, el gráfico de cantidad-tiempo, y basándose en supuestos geométricos, se puede deducir la siguiente ecuación de costo total de inventario:

  

  
  

  
  

  Debido a que se debe enunciar la solución en función de la demanda, y la gráfica está en función del tiempo, se procede a expresar la ecuación en función de tiempo:

  
  

  

  
  

  Esta ecuación, permite conocer el costo en función del tiempo, la investigación de operaciones es una herramienta para optimizar los valores de estas funciones dadas. Este punto óptimo se alcanza al proyectar el punto más bajo de la curva de costo de producción anual (Ctanual)hacia el punto de intersección entre las gráficas de costo por pedir y costo por mantener inventario. 

  

  
  

  Para ello se deben aplicar los criterios de optimización, mediante derivar la ecuación en base al valor a optimizar:

  
  

  

  
  

  Este es el resultado de optimizar la función de costos en función de la cantidad de la cantidad de material.
  

   

  Modelo EOQ con faltante planeado

  Este modelo, se rige por los mismos postulados que el anterior, la única diferencia es que este admite falta de producto.

  

   

  Según el modelo EOQ, se conocen los valores del costo de la adquisición de productos (CuQ) el costo de pedirlo (Cp) y el costo de inventario (Cmi). S es el faltante que se incurre al no poder satisfacer el pedido en su totalidad, por ello existe un costo por la cantidad que falta (Cf).

  Teniendo en cuenta, el gráfico de cantidad-tiempo, y basándose en supuestos geométricos, se puede deducir la siguiente ecuación de costo total de inventario:

  

  
  

  Debido a que se debe enunciar la solución en función de la demanda, y la gráfica está en función del tiempo, se procede a expresar la ecuación en función de tiempo:

  
  

  

  
  

  Esta ecuación, permite conocer el costo en función del tiempo, la investigación de operaciones es una herramienta para optimizar los valores de estas funciones dadas, es por ello necesario optimizar estas ecuaciones con el fin de obtener los valores más relevantes de cantidad y faltante.

  
  

  

  
  

  Este es el resultado de optimizar la función de costos en función de la cantidad de producto a pedir, es decir basado en la cantidad económica de pedido optimizando tanto cantidad como faltante.
  
  

  Modelo EOQ con descuento por cantidades

  
  

  
  

  El modelo EOQ con descuentos por cantidad, se basa en que dependiendo de cuanto producto se compre, se hará un descuento a ese producto. Este modelo toma en consideración precios distintos para distintas cantidades de producto, teniendo en cuenta que  el costo de mantener inventario y de pedir se mantienen, ambos, constantes.

  
  

  Las empresas manejan este modelo de inventario debido a que sus costos le permiten realizar este tipo de compras, que generan una reducción del precio de venta en el producto fabricado, o un ahorro para la empresa. Este modelo les proporciona sus costos totales más bajos según sus necesidades y los recursos con los que cuenten.

  Este modelo sigue las mismas fórmulas de EOQ sin faltante planeado para la cantidad óptima y para costo total anual.

  
  
  
  

   
  
  

  
  

  
  

  
  

  
  

  
  

  Para explicar mejor este modelo, se debe acudir a un ejemplo.

  
  

  
  

  
  
  EJEMPLO

  Teniendo un costo de pedir de $49, un porcentaje de 20% para mantener inventario y una demanda de 5000 unidades al año, se da la siguiente tabla de descuentos por unidad.

  
  

  Cantidad	Descuento (%)	Cu($)
  0-999	0	5
  1000-2499	3	4.58
  >2500	5	4.75

  
  

  Con la fórmula de cantidad óptima del modelo EOQ sin faltante se calculan las cantidades óptimas según cada precio. En la siguiente tabla se resumen.

  
  

  Cantidad	Q*
  0-999	700
  1000-2499	711
  >2500	718

  
  

  En tal caso, la cantidad óptima será 700 unidades, por ello se procede a calcular el costo anual con esta cantidad para el intervalo que la contiene, pero con la mínima cantidad para los intervalos mayores, la siguiente tabla resume los resultados:

  
  

  Cantidad	Cta
  0-999	25700
  1000-2499	24980
  >2500	2503550

  
  

  
  

  Por ello, el costo menor pertenece al intervalo de 1000 a 2499 unidades, pero la cantidad óptima no pertenece a este intervalo, por ello la cantidad a pedir será el límite inferior del intervalo. Es decir se pedirán 1000 unidades.

  
  

  
  

  Modelo EOQ con demanda probabilística

  
  

  
  

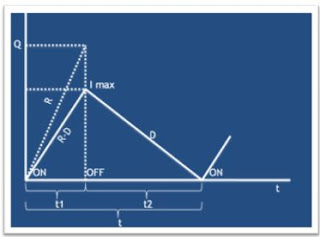
  Con el pasar del tiempo se ha tratado de adaptar el modelo determinístico de cantidad económica  de pedido EOQ para que refleje la naturaleza probabilista de la demanda, usando una aproximación que sobrepone una existencia constante de reserva sobre el nivel de inventario. El tamaño de la reserva (punto de reorden) se determina de tal modo que la probabilidad de que se agote la existencia durante el tiempo de entrega (el periodo entre la colocación de la orden y la recepción del pedido) no sea mayor que un valor especificado.

  
  

  La hipótesis principal de este modelo es que la demanda durante el tiempo de entrega, tiene una distribución normal, con media μ y desviación estándar σ. (μ se define como la demanda promedio durante el tiempo de entrega y σ es la desviación estándar de la demanda durante este mismo periodo).

  
  

  
  

  

  
  

  
  

  El valor promedio de  la demanda, la cual podemos ver ubicada en el punto medio de la curva de distribución normal, nos da a saber que existe  una probabilidad de que  en el 50% de las veces nuestro inventario no podrá satisfacer los requerimientos del mercado. Por tal razón al implementar este sistema de inventario, se debe establecer en primera instancia un porcentaje tolerable de error (α= probabilidad  máxima admisible de que se agote la reserva durante el tiempo de entrega), en otras palabras un número de veces en el que se es permitido que la demanda supere nuestras reservas y no se pueda satisfacer con las exigencias del mercado.

  
  

  Dos números críticos dentro de este sistema son, el  punto de reorden (R)  y la cantidad a pedir (Q). La política de inventario se puede resumir en estas dos variables, de la siguiente manera: Siempre que el nivel de inventario de un producto baje a R unidades, se coloca una orden de Q unidades para reabastecer el inventario. Estas dos variables se ven condicionadas por el tiempo de entrega (L), periodo en el cual la fluctuación de la demanda determinará el punto mínimo de  unidades a mantener en inventario. Q se determinará como se venía haciendo en el modelo básico de EOQ

  
  

  En resumen las variables de este modelo son: 

  
  

  L= tiempo  den entrega entre la colocación de la orden y la recepción del pedido.

  μL = Demanda promedio durante el tiempo de entrega.

  σL = Desviación estándar de la demanda durante el tiempo de entrega

  R = Punto de reorden (tamaño de la existencia de reserva).

  α= Probabilidad máxima admisible de que se agote la existencia durante el tiempo de entrega. 

  
  

  
  

  La demanda durante el tiempo de entrega L se suele describir con una función de densidad de probabilidades por unidad de tiempo (es decir por día o por semana), a partir de la que se puede determinar la distribución de la demanda durante L. Dado que la demanda por unidad de tiempo es normal, con media D y desviación estándar σ, la media μL y la desviación estándar σL de la demanda, durante el tiempo de entrega L, se calculan como sigue: 

  
  

  

   
  
  

  El punto de reorden entonces lo definimos como:

  
  

  

  
  
  
  
  

  En donde el valor de Z se encuentra en las tablas de distribución normal y toma el valor de Z = 1-α

  
  

  
  

  

  
  

  
  
  
  
  
  MODELO LEP
  Lote
  Económico de
  Producción
  
  
  El modelo LEP considera variables importantes como la tasa de producción y el costo de ordenar una operación y se centra en procesos industriales.
  
  
  Modelo LEP sin faltante planeado
  
  
  En este modelo se considera que la tasa de producción (R) es mayor que la demanda (D) y se toma en cuenta que existe un costo por generar una orden de producción. En este caso se prohíben los faltantes estableciendo el costos por faltantes como infinito. Las condiciones para este aprovisionamiento instantáneo de los  insumos se modifican ligeramente cuando los suministros se manufacturan al recibir la orden, en vez de que se surtan de existencias de artículos ya manufacturados.
  
  

  Niveles de inventario en un Modelo LEP sin faltante

  
  
  
  
  
  
  

  Teniendo en cuenta, el gráfico de cantidad-tiempo, y basándose en supuestos geométricos, se puede deducir la siguiente ecuación de costo total de inventario.

  
  
  
  
  
  
  
  
  
  
  
  
  
  
  Para expresar la anterior ecuación en función del tiempo, se divide en ambos lados de la ecuación por la expresión que determina el tiempo en que es entregado un pedido. De dicha ecuación, se procede a derivar  con respecto a Q con el fin de obtener el óptimo para el modelo:
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  Tomando en cuenta la derivada para el costo total de inventario en función del tiempo se procede a establecer una expresión que determine el óptimo para este modelo:
  
    
  
  
  
  
  
  
  
  
  
  
  
  Modelo LEP con faltante planeado
  
  
  Esta extensión de EOQ permite que existan faltantes y se cumplan las entregas atrasadas, suponiendo que exista un nivel mínimo de atraso que la administración esté dispuesta a tolerar. Los faltantes ocurren en el sistema de producción por falta de material, falta de capacidad o ambas.
  
  

  Niveles de inventario en un Modelo LEP con  faltante.

  
  
  De la gráfica anterior se pueden hacer deducciones geométricas que se muestran a continuación:
  

  

  
  
  Al derivar parcialmente con respecto a Q y a S, se obtiene el óptimo del modelo, que se encuentra representado por las siguientes expresiones:
  
  
  
  
  
  
  

  
  

  Reglas de la gestión de inventarios

  
  

  1.   TODA entrada o salida de inventario debe ser debidamente documentada.
  
  

  2.   TODO ítem debe estar debidamente codificado, localizado y sistematizado.
  
  

  3.   TODOS los ítems deben estar guardados en el mismo lugar, de ser posible.
  
  

  4.   NUNCA recibir comisiones de un proveedor.
  
  

  5.   En cuanto sea posible, el lugar físico donde se realiza la recepción de materiales, debe ser DIFERENTE a donde se encuentra la salida de materiales.
  
  

  6.   Los ítems deben estar ordenados de mayor peso de abajo hacia arriba.

  7.   TODO movimiento debe estar diferenciado entre entrada y salida.
  
  

  8.   NINGÚN miembro del equipo de almacén se puede ir , hasta que no haya un ESTRICTO conteo físico de los ítems que han entrado y salido.
  
  

  9.   Cuando se esté haciendo el conteo físico, se debe hacer por tres auditorios diferentes y se consignan los que tengan dos lecturas iguales. De lo contrario un auditor contará en presencia de los otros dos.
  
  

  10.               El punto más lejano en el lugar de almacenamiento debe tener un EXTINTOR.
  
  

  11.               Los reportes de inventarios deben estar como máximo tres días después del ciclo del periodo contable.